
Photo by Volkan Olmez on Unsplash
Demystifying Floating Point Numbers: How Computers Store and Handle Them
Exploring the Inner Workings and Challenges of Floating Point Representation
Last week when I was having lunch, I suddenly thought of how floating point numbers are stored in binary representation. Even though I've been programming for a while, I couldn't remember and took this for granted. Let's dive into this basic idea together. We'll explore how computers use binary to represent numbers and maintain accuracy in calculations.
Understanding decimal and binary representation
Decimal is one of the common ways we represent numbers in our daily life, it contains digits from 0-9. The position of each number represents its value, with each position representing a power of 10(decimal is base-10). For example, in the number 123, the digit 3 represents the ones place(10^0), the digit 2 represents the tens place (10^1), and the digit 1 represents the hundreds place (10^2).
This idea of representing numbers with a base can be extended to other base values like, binary - 2, hexadecimal - 16 and so on..
This sounds good, but how do we use this type of notation to represent fractions. This is supported in the notation by having a . in the number, the numbers prior to the . are similar to what we've discussed earlier. Whereas a number after . represents the fractional portion. In the fractional portion each number represents a negative power of 10(for decimal). For example, in the fractional portion of 123.45 the digit 4 is in the tenths place (10^-1) and the digit 5 is in the hundredths place (10^-2).
Can we expand this to binary?
The answer is yes.
For example:
$$123_{10} = 1111011_{2}$$
$$123.45_{10} =1.1110110111\overline{0011}_{2}$$
$$1.25_{10} = 1.01_2$$
Storing the whole number part of a binary number is pretty straight forward, but how are we going to store the fraction part of the binary in a computer?
Different ways of representing a given number
The notation that we were reading about earlier is the general notation(decimal notation) that we use in our daily life. There are other types of notation such as scientific notation, in this notation any non-zero numbers is written in the form
$$m * 10^{n}$$
For example, following are all valid notations for the number 123
1.23 * 10^2
12.3 * 10^1
123 * 10^0
0.123 * 10^3
Among the above examples, the first one is called the standard scientific notation as there is only one non-zero number before the decimal point. Following are few other examples in standard scientific notation
5 * 10^1
9.214 ^ 10^-7
This scientific notation can be extended to binary, which is what the IEEE 754 is.
Understanding IEEE754
IEEE 754 Floating point arithmetic is a technical standard established in 1985. In this format a floating point number is represented by a sign s, exponent e, fraction f.
Following is the structure of how these components are stored in-memory.
| Sign | Exponent | Fraction | |
| Single precision (32-bit) | 1 [31] | 8 [30-23] | 23 [22-00] |
| Double precision (64-bit) | 2 [63] | 11 [62-52] | 52 [51-00] |
Other precision format's can be found here.
Let's understand each component in more detail:
Sign
This is the sign of the number represented in bit, 1 is negative and 0 is positive.
Exponent
This is the exponent part of the number in the standard scientific notation of the number. For single precision exponent has 8 bits, as there is no dedicated bit to store the sign of the exponent hence we have an offset value that helps us to get actual exponent. For single precision this value is 127. For example, if we want to store the exponent as -2, we'll be storing it as 125(-2+127) in memory. For 0 exponent this value would be 127.
For double precision we have 11 bits to store the exponents, hence the offset for it is 1023.
Fraction
In a standard scientific notation the value before the decimal point should always be 1(as it should be non-zero). We don't store this part in memory, instead we assume it by default. The value after the decimal point is stored in memory, for a single precision the fraction has 23 bits, and for double precision the fraction has 52 bits.
Let's look at a few example to see what we've learnt.
- 123 is represented as:
$$1.23 * 10^2 = 1.111011 * 2^6 $$
$$ 0 | 10000101 | 11101100000000000000000$$
- -1.25 is represented as:
$$-1.25 * 10^0 = -1.01 * 2^0 $$
$$ 1|01111111|01000000000000000000000$$
Among, all the 3 parts that are discussed, fraction has an interesting problem. There is sometimes a chance a floating point number has a repeating decimal part, for example 123.45 in binary, it has a repeating portion 0011 when storing this number in the above format the number, the binary needs to be truncated to 23 bits(for single precision) which would result in a small error when converting the number back. This error is called precision, the larger the number of bits allocated to fraction the lower the precision value.
Let's try to understand this by example, for the number 123.45 the IEE 754 format is
$$1.2345 * 10^2 = 1.1110110111\overline{0011} * 2^6 $$
$$ 0 | 10000101 | 11101101110011001100110$$
If we convert the IEEE 754 value back to decimal we get, 123.4499969482421875 the error here is 0.0000030517578125.
This error is why this meme exists.
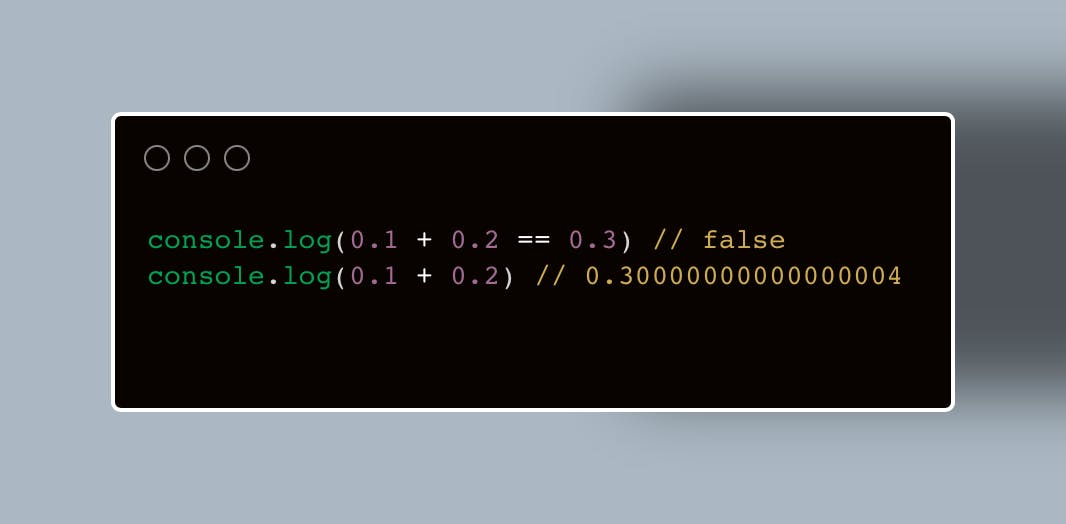
So while doing a floating point math in your program, we must always consider an error. This error is already present in your language by default, for example Number.EPSILON in javascript.
References:
IEEE 754 - https://en.wikipedia.org/wiki/IEEE_754#Basic_and_interchange_formats
IEEE 754 Convert - https://www.h-schmidt.net/FloatConverter/IEEE754.html
